Chapter 11 Calculus and Physics
Philosophy is written in this grand book, which stands continually open before our eyes (I say the ‘Universe’), but can not be understood without first learning to comprehend the language and know the characters as it is written. It is written in mathematical language, and its characters are triangles, circles and other geometric figures, without which it is impossible to understand a word; without these one is wandering in a dark labyrinth.
— Galileo Galilei
This is the final chapter of this textbook. We hope you have enjoyed this journey; we certainly enjoyed creating this textbook. We conclude this textbook with a study of the profoundly, surprisingly, enchantingly deep connection between Calculus and the physical world. We will show that we can derive formulas for the motion of planets, projectiles, light, fluids, and the behavior of electrical circuits.
11.1 Kinematic Equations and Newton’s Laws
As our first foray into mathematical physics, we will discuss kinematics, which is simply a study of objects which have no forces applied to them except the force applied to begin motion. These objects have constant acceleration and admit some simple formulas to describe them. Then, we will state and apply Newton’s Laws of Motion
11.1.1 Speed and Acceleration in Physics
One of the most important advances humans have ever made is the notion that one can apply mathematics to describe the behavior of the world. Isaac Newton was the first to fully realize the connection between Calculus and the natural world. More precisely, he demonstrated that speed can be encoded using the first derivative, while acceleration can be encoded using the second derivative. Below is a diagram of the position of a car over time.
Notice that whenever the slope of the line is positive, the car is moving to the right. The slope of the orange line is given by the derivative with respect to time. In other words, the car is moving right if
\[\frac{dx}{dt} > 0 \Rightarrow \text{Car moves right}\]
On the other hand, while the slope is negative, the car is moving to the left. That is, we have
\[\frac{dx}{dt} < 0 \Rightarrow \text{Car moves left}\]
Notice also that when the derivative of the position is zero, the car is stationary. That is, we have
\[\frac{dx}{dt} = 0 \Rightarrow \text{Car is stationary}\]
Therefore, the first derivative tells us the speed of the car and the direction it is moving. We can extend this idea further: if the first derivative is speed, the second derivative is the acceleration of the car.
11.1.2 x and y components
Another important aspect of kinematics in two dimensions is dividing the \(x\) and \(y\) components of motion. Suppose we have two balls: one that was dropped and another that is given a throw to the right. This is illustrated below:
Notice that the thrown ball falls as rapidly as the ball that was dropped.
11.2 Range of Projectiles
Imagine we are firing cannonballs. We want to maximize the range that the cannonball travels. At what angle should we fire the cannonball to maximize the distance it travels? We have control over the initial firing speed \(v_0\) and the angle at which the cannonball is fired, \(\theta\). Consider the diagram below.
We want to prove that, no matter the initial firing speed \(v_0\), the angle at which the range \(R\) is maximized is \(45^{\circ}\). When the cannonball is initially fired, it has an \(x\) and a \(y\) component to its velocity, as illustrated below.
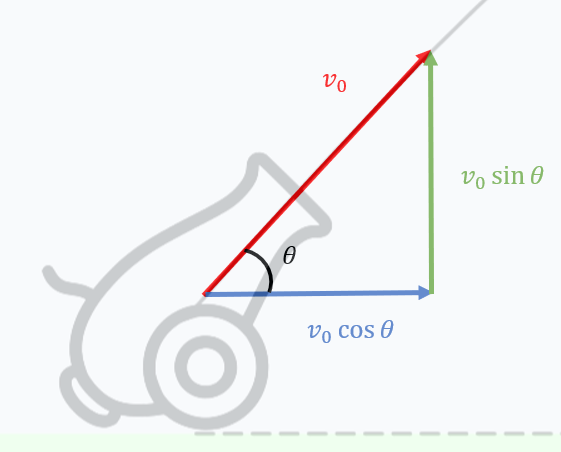
As was described in the previous section, the acceleration downward everywhere on earth is approximately \(g = -9.8 \frac{m}{s^2}\). We will also neglect air resistance, which would affect the acceleration of our cannonball as air molecules bump into it. With all of this in mind, our first equation is given by
\[\frac{d^2 y}{dt^2} = -g \]
Because there is no \(x\)-component force on the cannonball other than the initial force applied to get the cannonball moving, its speed will be the same until it hits the ground (Newton’s First Law). Hence, the equation will look like the following:
\[\frac{dx}{dt} = v_0\cos\theta\]
We will integrate the first equation twice and the second equation once. For the \(y\)-component, we integrate once to obtain
\[\frac{d^2 y}{dt^2} = -g \Rightarrow v_y(t) = \frac{dy}{dt} = C - gt\]
Where \(C\) is our constant of integration. If we plug in zero in the right equation above, then we are asking the equation to tell us what the initial y component of the speed is. That is, we have
\[v_y(0) = C - g\cdot 0 = C\]
Therefore, our equation becomes
\[\frac{dy}{dt} = v_y(0) - gt\]
Integrating once more, we obtain
\[y(t) = C + v_y(0)t - g\int_{0}^{t} t' \, dt' = C + v_y(0)t - \frac{1}{2}gt^2\]
Now if we plug in \(t = 0\), we are asking the equation to tell us the initial height of the cannon above the ground. In this example, we are assuming that the ground is totally level, so that the height of the cannonball when it lands will be the same as that of the cannon. Therefore, we have:
\[0 = y(0) = C + v_y(0)\cdot 0 - \frac{1}{2} g (0)^2 = C\]
We know from the diagram above that \(v_y(0) = v_0\sin\theta\). Therefore, our final equation is
\[y(t) = y(0) + v_y(0)t - \frac{1}{2} g t^2 = \boxed{(v_0\sin\theta) t - \frac{1}{2}gt^2}\]
Integrating the \(x\)-component equation, we have
\[v_x(t) = \frac{dx}{dt} = v_0\cos\theta \Rightarrow x(t) = C + (v_0\cos\theta)t\]
At \(t = 0\), the cannonball hasn’t been fired from the cannon yet, so it hasn’t traveled anywhere. Therefore, we have
\[0 = x(0) = C \Rightarrow x(t) = \boxed{(v_0\cos\theta)t}\]
Our goal was to determine where the cannonball lands. This happens when the cannonball has hit the ground, or \(y(t) = 0\). Therefore, we set \(y(t)\) equal to zero to determine the time when the cannonball hits the ground:
\[y(t) = (v_0\sin\theta)t - \frac{1}{2}gt^2 = 0 \Rightarrow (v_0\sin\theta)t = \frac{1}{2}gt^2 \]
Solving this equation for \(t\), we find the time when the cannonball hits the ground:
\[t_R = \frac{2v_0\sin\theta}{g}\]
Now, our goal was to find the distance the cannonball travels. Therefore, we can plug in \(t_R\) into the equation above to obtain
\[R = x(t_R) = (v_0\cos\theta)\frac{2 v_0\sin\theta}{g} = v_0^2\cdot \frac{2\sin\theta\cos\theta}{g}\]
We learned in Chapter 1 that \(2\sin\theta\cos\theta = \sin(2\theta)\) (@ref(#MoTrigIdent))
11.3 Period of a Pendulum
We can use differential equations to determine the behavior of pendulums, too. Oscillators of all sorts appear in physics, and a pendulum is an interesting first example.
11.4 Principle of Least Time and Snell’s Law
We next direct our attention to light. In modern physics, light can be shown to possess properties of both waves and particles. One of the most fascinating features of light is its tendency to bend in going from one medium (like air) to another (like water). This bending of light in going from one medium to another is called refraction.
In science, we are never satisfied only with the observation of some phenomenon. We seek to construct models that allow us to predict the way a system will behave for certain configurations. Within such a model, we postulate certain rules that the system obeys then use experiments to determine how well the system obeys the rules we’ve imposed on it. Pierre de Fermat suggested such a rule called The Principle of Least Time to explain some of light’s behaviors.
As in the diagram above, suppose I have two points labelled \(A\) and \(B\) and that a beam of light will be travelling between these two points. Suppose further that the light is travelling between two transparent media: glass and water, air and water, water and diamond, and so on. In travelling from \(A\) to \(B\), we might suppose that the light will travel along a straight line between those points because it is the shortest path, thus it is reasonable to suspect that it would be the path of least time. However, you can observe that light does not follow such a path if the light encounters a boundary between two different transparent media. In fact, it follows a bent path.
Using the Principle of Least Time and a little Calculus, we can explain why light bends in travelling from one transparent medium to another. We will need one more fact which
11.7 The End!
You have finished the text! How should you proceed from here?
There are several subjects which you should now be prepared to tackle. Below, we provide a list of subjects in mathematics that you can study next, a description of each subject, and textbooks/materials we feel will help you understand each subject.
Multivariable Calculus
Linear Algebra
Differential Equations
Fourier Analysis
Real Analysis
Abstract Algebra
Algorithms
Mathematical Statistics/Probability
Complex Analysis
Modern Mechanics
Quantum Mechanics