Chapter 7 Integral Applications
The most beautiful experience we can have is the mysterious. It is the fundamental emotion that stands at the cradle of true art and true science…
— Albert Einstein
We have now built quite a bit of mathematical machinery with which to solve problems. This represents a turning point of the textbook, when we switch from learning tools to applying those tools.
7.1 Computing Arc Lengths
Up to this point, we have only really considered integration as a means of computing areas. In fact, we can use integration in all sorts of context. In this first section, we show how we can use integration to compute the lengths of arbitrary plane curves. The following illustration demonstrates how we think about computing the arc length of a curve with integrals:
As usual with integration, the main idea is to chop up the object of interest (in this case, the function’s shape) and approximate each little piece with something whose length or area we can easily compute. In this case, it’s quite easy to compute the distance between two points on a straight line; therefore, we divide the function of interest into pieces and approximate each piece with a line segment. This is what is being illustrated in the figure above.
After the object has been finely chopped, we add up the little segments. Then, we let the number of these little segments go to infinity (and let the segments become arbitrarily short). Upon letting each segment become arbitrarily short and the number of such segments become large, the sum turns into an integral.
Artists are not satisfied with the mere concept of a painting. They have to use their easel and their paints and their brushes to realize an idea. Similarly, a mathematician is never satisfied with only concepts. We must express our thoughts in notation. This can be a little intimidating at first, but it will allow us to compute more about the world than we could without the notation.
Consider the diagram below. We define a new differential element, which we call \(ds\). This corresponds to one of the tiny segments which is used to approximate a curved section of a given function as illustrated above. We must imagine that this element is very small; indeed, we let its length go to zero.
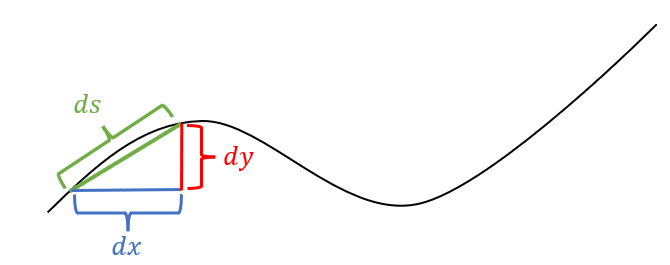
By the Pythagorean Theorem, \(ds^2 = dx^2 + dy^2\). Ultimately we will be summing up many segments with length \(ds\), so we want to isolate it. We have
\[\begin{equation} ds = \sqrt{dx^2 + dy^2} \tag{7.1} \end{equation}\]
Now we integrate over all little slices \(ds\). Upon doing this, we will have the desired length of the curve. But first, we must remove one of the \(dx\) so we have something to integrate on the right hand side. To this end, we have
\[ds = \sqrt{dx^2\left(1 + \left(\frac{dy}{dx}\right)^2 \right)} = dx\sqrt{1 + \left(\frac{dy}{dx}\right)^2}\] Now we can integrate. The left side will be the arc length. The bounds on the right will be from \(a\) (the left endpoint) to \(b\) (the right endpoint):
\[L = \int \, ds = \int_{a}^{b} \sqrt{1 + \left(\frac{dy}{dx}\right)^2} \, dx\]
That’s our formula! Note that we define \(y = f(x)\), so \(\frac{dy}{dx}\) is simply the derivative of the function whose length we’re interested in computing. The example below illustrates how we use this formula to compute arc lengths.
Example 7.1 (Arc Length Example 1) Compute the arc length of the function \(y = f(x) = x^{\frac{3}{2}}\) from \(a=1\) to \(b=4\).
First, we compute the derivative of the function whose arc length we wish to compute. We have:
\[\frac{dy}{dx} = \frac{3}{2}x^{\frac{1}{2}} \Rightarrow \left(\frac{dy}{dx}\right)^2 = \frac{9}{4}x\] Therefore, the desired arc length is given by the integral
\[L = \int_{1}^{4} \sqrt{1 + \frac{9}{4}x}\, dx\]
This integral can easily be solved using u-substitution, (6.2). We let \(u = 1 + \frac{9}{4}x\), so \(du = \frac{9}{4} dx \Rightarrow dx = \frac{4}{9} du\). Therefore, our integral becomes
\[L = \int_{\frac{13}{4}}^{10} \sqrt{u} \frac{4}{9} \, du = \frac{4}{9}\int_{\frac{13}{4}}^{10} u^{\frac{1}{2}} \, du = \frac{4}{9}\left[ \frac{2}{3}u^{\frac{3}{2}}\right]_{\frac{13}{4}}^{10} \approx 7.6337\]
Note that the illustration above has a sequence that converges to this value as the \(n\) slider approaches infinity.