Chapter 9 Polar Coordinates and Calculus
It is impossible to be a mathematician without being a poet in soul.
— Sofya Kovalevskaya
9.2 Changing coordinate systems
Up to this point we have imposed a Cartesian Coordinate system on a plane to do our analyses. The Cartesian Coordinate system splits the plane into a grid of little rectangles that we can use to identify positions of points and produce plots. Not all phenomena we wish to describe are easily decomposed into a grid of rectangles, however. For instance, gravity extends radially inward from all directions. Any object along a circle a distance \(r\) from the object of interest experiences the same force of gravity. The graphic below illustrates this:
Notice that by Newton’s Law of Gravity, the force of gravity depends spatially only on the distance \(r\), not on the \(x\) and \(y\) coordinates. Indeed, if we wanted to re-express Newton’s Law of Gravity in terms of rectangular (occasionally also called Cartesian) coordinates, the formula would be \(F = G\frac{Mm}{\sqrt{x^2 + y^2}}\), which is significantly more ugly than the formula \(F = G\frac{Mm}{r^2}\) in polar coordinates.
For the remainder of this chapter, we will impose polar coordinates onto the plane. Instead of having an \(x\) value to specify a horizontal direction and a \(y\) value to specify a vertical direction, we have a distance \(r\) from the origin and an angle \(\theta\) specifying the amount our point has orbited the origin. The following illustration depicts this idea:
A critical thing to notice is that the points of the plane are not uniquely specified by polar coordinates as they are for rectangular coordinates. Because a circle repeats every \(2\pi\) radians (1.3.2), the point \((2, 0)\), \((2, 2\pi)\), and \((2, 4\pi)\) all specify the same point. This is totally different than rectangular coordinate, where each point is associated with a single point \((x, y)\).
There is a relationship between rectangular coordinates and polar coordinates.This illustration is provided below:
Note that \(x\), \(y\), and \(r\) form a right triangle. Therefore, by the Pythagorean Theorem, we have
\[\begin{equation} r^2 = x^2 + y^2 \Rightarrow r = \pm\sqrt{x^2 + y^2} \tag{9.1} \end{equation}\]
We also want a formula to determine \(\theta\). As is evident from the illustration, we have:
\[\begin{equation} x = r\cos\theta\hspace{3mm}\text{and}\hspace{3mm} y = r\sin\theta \tag{9.2} \end{equation}\]
We can divide \(y\) by \(x\) to obtain
\[\frac{y}{x} = \frac{\color{red}{r}\sin\theta}{\color{red}{r}\cos\theta} = \frac{\sin\theta}{\cos\theta} = \tan\theta\]
Therefore, our other equation is
\[\begin{equation} \tan\theta = \frac{y}{x} \Rightarrow \theta = \tan^{-1}\left(\frac{y}{x}\right) \tag{9.3} \end{equation}\]
An important thing to note from (9.1) is that we do allow \(r\) to be negative. What this means is that \(-r\) goes through the origin and is the same length as \(r\). The illustration below gives the idea:
For everything we’ve done thus far, functions took the form \(y = f(x)\) (or occasionally \(x = f(y)\)). That is, our function takes in numbers from the \(x\)-axis and returns outputs that determine the \(y\)-coordinate. Now our functions will be of the form \(r = f(\theta)\). That is, the angle will be the input while the distance from the origin will be output.
9.3 Plotting Functions in Polar Coordinates
We are now going to show you what certain plots look like it polar coordinates. Don’t worry about memorizing them, you can use this section as a reference. After we have illustrated what each polar equation looks like, we will describe how you can produce such curves using pencil and paper. Then, we will use Calculus to determine the length and area of polar curves.
Lines
How do we describe lines in polar coordinates? Notice that each angle measure on the plot of polar coordinates corresponds to a line radiating from the origin. Therefore, if we are interested in a line going through the origin an angle \(\alpha\) from the \(x\)-axis, then the equation of the line is given by
\[\theta = \alpha\] How does this translate to a line in rectangular coordinates? From (9.3), we know that \(\theta = \tan^{-1}\left(\frac{y}{x}\right)\). Therefore, we have
\[\alpha = \theta = \tan^{-1}\left(\frac{y}{x}\right) \Rightarrow \tan\alpha = \frac{y}{x} \Rightarrow y = \left(\tan\alpha\right)\cdot x\]
Unfortunately, Desmos does not currently permit the plotting of \(\theta = \alpha\) directly. However, we can plot \(y=(\tan\alpha)\cdot x\) which implies the former:
We established that \(x = r\cos\theta\) and \(y = r\sin\theta\). A vertical line running through the point \((a, 0)\) is given by \(x = a\) in rectangular coordinates. Therefore, in polar coordinates, a vertical line is given by
\[a = x = r\cos\theta \Rightarrow r = \frac{a}{\cos\theta}\]
This formula is illustrated below.
Using the formula for \(y = r\sin\theta\), we can draw out horizontal lines in polar coordinates, too. A horizontal line running through point \((b, 0)\) in rectangular coordinates is given by \(y = b\). Therefore, in polar coordinates, a horizontal line is given by
\[b = y = r\sin\theta \Rightarrow r = \frac{b}{\sin\theta}\]
Conic Sections
We can also produce the conic sections easily using polar coordinates.
Circles
Considering the entire basis of polar coordinates is founded upon circles, it will probably come as no surprise there are many way to describe circles in polar coordinates.
Recall that the definition of a circle is all of the points a distance \(r\) from the circle’s center \(C\). Recall also that the distance from the origin is \(r\) in polar coordinates. Therefore, the equation
\[r = a\]
Are all of the points a distance \(a\) from the origin, which is a circle. This is illustrated below.
BORING! There are other ways to draw circles in polar coordinates. As illustrated below, the formula
\[r = 2k\cos\theta\] plots a circle of radius \(|k|\) centered at \((k, 0)\). The illustration should be illustrative in illustrating this:
Hence, with \(\cos\theta\), the circle opens along the \(x\)-axis. If we replace \(\cos\theta\) with \(\sin\theta\), the circle opens along the \(y\)-axis. The equation is given by
\[r = 2m\sin\theta\]
which plots a circle of radius \(|m|\) centered at \((m, 0)\). The following depiction depicts this with a picture:
You might wonder what would happen if you combine the two previous formulas. It produces another circle! That is,
\[r = 2k\cos\theta + 2m\sin\theta\]
produces a circle centered at \((k, m)\) with radius equal to \(\sqrt{k^2 + m^2}\). This is illustrated below:
There is a formula in polar coordinates that allows us to plot all conic sections at once. It is given by
\[\begin{equation} r = \frac{a}{1 + e\cos\theta}, \tag{9.4} \end{equation}\]
where \(a\) is the amplitude while \(e\) is the eccentricity. When the eccentricity \(e = 0\), then the equation reduces to \(r = a\), which is equivalent to the first equation of a circle provided above.
Ellipses
If \(-1 < e < 1\) in (9.4), then the equation produces an ellipse. This is illustrated below. Play with both the eccentricity and the amplitude to see how the shape changes as these parameters are changed (NOTE: because \(e\) is reserved for Euler’s Constant, \(e = 2.7178281828...\), we use \(k\) for the eccentricity instead. We hope this does not confuse the reader):
Parabola
Meanwhile, if \(e = 1\) or \(e = -1\) in (9.4), then the equation produces a parabola. Once again, we replace \(e\) with \(k\) since \(e\) is reserved for Euler’s constant. Play with the illustration below to understand how the shape of a parabola changes for different amplitudes and eccentricities:
Hyperbola
Finally, if \(|k| > 1\) in (9.4), then the equation produces a hyperbola.
Notice that if we are interested in hyperbolas, we require the magnitude of \(k\) to be greater than \(1\).
Cardioids
We can easily make more complicated shapes in polar coordinates. The first example of these more complicated shapes is the cardioid. In Greek, cardi is a prefix meaning heart, while oid is a suffix meaning resembling or in the shape of. Therefore, the cardioid is in the shape of a heart, as the following illustration demonstrates.
As shown in the illustration above, the cardioid can be produced by rotating one circle about another. Cardioids along the \(x\)-axis can be produced by the equation
\[ r(\theta) = a\pm a\cos\theta\]
The plot produced by these equations is illustrated below. When \(n = 1\), we are plotting the equation \(r = a + a\cos\theta\). On the other hand, when \(n = 2\), we are plotting \(r = a - a\cos\theta\).
A very similar equation produces a cardioid along the \(y\)-axis. Its equation is given by
\[r(\theta) = a \pm a\sin\theta\]
This is identical to the equation above with cosine replaced with sine. The illustration of this equation is provided below.
Limaçons (Snails)
Limaçons are just general forms of cardioids. Just like cardioids, we can have limaçons which open along the \(x\)-axis and limaçons which open along the \(y\)-axis. The equation for a limaçon opening along the \(x\)-axis is given by
\[r = a \pm b\cos\theta\]
while a limaçon opening along the \(y\)-axis is given by
\[r = a \pm b\sin\theta\]
For both cases, we will assume that \(a, b > 0\). It is the ratio \(\frac{a}{b}\) which determines the shape of the limaçon.
Case 1: \(\frac{a}{b} < 1\)
In this case, the limaçon will have an inner loop, as illustrated below. These limaçons open along the \(x\)-axis.
We can also produce limaçons that open along the \(y\)-axis:
Case 2: \(\frac{a}{b} = 1\)
When \(\frac{a}{b} = 1\), then \(a = b\), in which case the shape of the graph is a cardioid. We dealt with cardioids in the previous section and will not explore them further here.
Case 3: \(1 < \frac{a}{b} < 2\)
In this case, the graph will still have a dimple, but it won’t be as sharp as it is for the cardioid. Furthermore, the dimple will not touch the origin as it does for the cardioid. Limaçons satisfying \(1 < \frac{a}{b} < 2\) are illustrated below.
Because the limaçon opens along the \(x\)-axis, its equation involves \(\cos\theta\). The same graph can open along the \(y\)-axis if we use \(\sin\theta\) instead:
Case 4: \(\frac{a}{b} \geq 2\)
In this case, we don’t have a dimple, but one side is flatter than the other. The illustration below shows what this curve looks like when opening along the \(x\)-axis:
As usual, we can replace \(\cos\theta\) with \(\sin\theta\) to change its orientation such that it opens along the \(y\)-axis:
Lemniscates
Next, we will analyze the lemniscate. It looks like an infinity sign or a figure eight. As was true for the other functions, the appearance of the graph changes depending on whether we use the sine function or the cosine function. The equations for lemniscates take the form
\[r^2 = a^2\sin 2\theta \hspace{2mm}\text{or}\hspace{2mm} r^2 = a^2\cos 2\theta\]
The first equation is illustrated below. Note that the lemniscate has two axes of symmetry. The one running through its length is the line \(\theta = \frac{\pi}{4}\):
The second equation is very similar to the first, but now the axis of symmetry along the lemniscate’s length is through the line \(\theta = 0\).
Rose Curves
The last of these polar curves will be the rose curves. These can be produced using equations of the form
\[r(\theta) = a\sin n\theta \hspace{2mm}\text{or}\hspace{2mm} r(\theta) = a\cos(n\theta)\]
The illustration below depicts the first formula:
Meanwhile, the following illustration depicts the second equation:
There are a few things to notice here. Regardless of whether the rose curve is produced by sine or cosine, when \(n\) is even, the rose has \(2n\) petals. That is, if \(n = 2\), the rose has \(4\) petals. On the other hand, if \(n\) is an odd integer, then the rose will have \(n\) petals. That is, if \(n = 3\), the rose will have \(3\) petals.
Another important observation is that a cosine rose petal always falls along the \(x\)-axis. You can use this to distinguish between a cosine rose curve and a sine rose curve.
Producing These Plots Yourselves
All of these illustrations are wonderful, but how would we produce such plots ourselves? Doing so is quite simple. The activity includes polar graph paper you can use to plot your own roses
Example 9.1 (Circle Plot Activity) Use the following polar coordinate graph paper to plot the function \(r(\theta) = 4\sin 3\theta\).
Download polarGraphPaper.pdfTo complete the activity, we first want to plot a set of points on our polar graph paper then connect them with a smooth curve. We imagine picking neat and simple angles \(\theta\) around the circle and compute the distance \(r\) for those angles. Because of the \(3\theta\) in the argument for sine, we will mostly pick angles whose denominators are multiples of \(3\). We begin by plotting the points for angles \(\theta_1 = 0 = 0^{\circ}\), \(\theta_2 = \frac{\pi}{12} = 15^{\circ}\), \(\theta_3 = \frac{\pi}{6} = 30^{\circ}\), \(\theta_4 = \frac{\pi}{4} = 45^{\circ}\), \(\theta_5 = \frac{\pi}{3} = 60^{\circ}\). Plugging in these angles to the formula \(r(\theta) = 4\sin 3\theta\), we have:
\[r(0) = 4\sin 3\cdot 0 = 0\]
\[r\left(\frac{\pi}{12}\right) = 4\sin 3\cdot \frac{\pi}{12} = 4\sin\left(\frac{\pi}{4}\right) = 2\sqrt{2}\]
\[r\left(\frac{\pi}{6}\right) = 4\sin 3\cdot \frac{\pi}{6} = 4\sin\left(\frac{\pi}{2}\right) = 4\]
\[r\left(\frac{\pi}{4}\right) = 4\sin 3\cdot \frac{\pi}{4} = 4\sin\left(\frac{3\pi}{4}\right) = 2\sqrt{2}\]
\[r\left(\frac{\pi}{3}\right) = 4\sin 3\cdot \frac{\pi}{3} = 4\sin\left(\pi\right) = 0\]
Therefore, we have points
\[(0, 0)\]
\[\left(\frac{\pi}{12}, 2\sqrt{2}\right)\]
\[\left(\frac{\pi}{6}, 4\right)\]
\[\left(\frac{\pi}{4}, 2\sqrt{2}\right)\]
\[\left(\frac{\pi}{3}, 0\right)\]
in polar coordinates.
Now that we have these points, we plot them on our paper:
Finally, we connect those points with a curve:
You can continue this process from \(\theta = 0\) to \(\theta = 2\pi\) to complete the entire curve.
9.4 Derivatives of Polar Plots
Just as we can compute and plot the derivatives of plots in rectangular coordinates, we can also compute and plot the derivatives of polar equations. A few examples are provided below.
Derivative of a Rose Curve
Derivative of a Limaçon
Derivative of an Ellipse
Strikingly, there is a single equation that allows one to find the plot of the derivative for all polar equations. How should we compute the derivative? Ultimately, if we wish to produce the lines in the illustrations above, we are looking for \(\frac{dy}{dx}\), not \(\frac{dr}{d\theta}\). The line describes how \(y\) changes when \(x\) changes, not how the distance \(r\) changes when \(\theta\) changes.
How do we compute \(\frac{dy}{dx}\)? We can use a clever trick. First note that we can rewrite \(\frac{dy}{dx}\) as
\[\frac{dy}{dx} = \frac{dy}{d\theta}\cdot\frac{d\theta}{dx} = \frac{dy/d\theta}{dx/d\theta},\]
where we flipped the second fraction over and put it in the denominator for the last quantity. We already saw (9.2) that \(x = r(\theta)\cos(\theta)\) and \(y = r(\theta)\sin(\theta)\). We can find the derivative of each of these quantities and put them in the fraction above, which will be the derivative we seek.
In particular, we use the product rule 3.4.2 to determine each of the derivatives:
\[\frac{dy}{d\theta} = \frac{d}{d\theta}\left[r(\theta)\sin(\theta)\right] = \frac{dr}{d\theta}\sin\theta + r(\theta)\cos\theta\]
\[\frac{dx}{d\theta} = \frac{d}{d\theta}[r(\theta)\cos(\theta)] = \frac{dr}{d\theta}\cos\theta - r(\theta)\sin\theta \]
Where we use the fact that \(\frac{d}{d\theta}\cos\theta = -\sin\theta\) 3.3.4 in the second equation. Having found these, the derivative we seek is given by
\[\begin{equation} \frac{dy}{dx} = \frac{dy/d\theta}{dx/d\theta} = \frac{\frac{dr}{d\theta}\sin\theta + r(\theta)\cos\theta}{\frac{dr}{d\theta}\cos\theta - r(\theta)\sin\theta} \tag{9.5} \end{equation}\]
This is wonderful that we have found the derivative, but how do we compute the line to plot it? We know that the point slope form of the line is given by the equation \(y = mx + b\). We know the derivative is equal to the slope of the tangent line, so that \(m = \frac{dy}{dx}\). We only need a single point to find the \(y\)-intercept \(b\). We know a point that lies on the curve, namely, \((r(\theta)\cos\theta, r(\theta)\sin\theta)\) because of (9.2). Therefore, the \(y\)-intercept is given by
\[ y = mx + b \Rightarrow r(\theta)\sin\theta = \frac{dy}{dx}r(\theta)\cos\theta + b \Rightarrow b = r(\theta)\sin\theta - \frac{dy}{dx}r(\theta)\cos\theta\]
Therefore, the tangent line for any polar curve is given by
\[y = \frac{dy}{dx}x + r(\theta)\sin\theta - \frac{dy}{dx}r(\theta)\cos\theta = \frac{dy}{dx}(x - r(\theta)\cos\theta) + r(\theta)\sin\theta\]
Plugging in (9.5), we finally have
\[y = \frac{\frac{dr}{d\theta}\sin\theta + r(\theta)\cos\theta}{\frac{dr}{d\theta}\cos\theta - r(\theta)\sin\theta}(x - r(\theta)\cos\theta) + r(\theta)\sin\theta\]
9.5 Computing Areas of Polar Functions
Integration in polar coordinates is very similar to integration in rectangular coordinates. Appropriately, when integrating in rectangular coordinates, we approximate the area of the curve in which we’re interested with rectangles. On the other hand, when we are integrating polar curves, we use circular arcs to approximate areas. We let each circular arc become very narrow and allow the number of circular arcs to become very large. The illustration below depicts how to integrate \(r(\theta) = 4\sin 3\theta\), the polar curve we plotted above:
We establish a partition of the input \(\theta\) just as we partition the input \(x\) in rectangular coordinates. We are integrating from \(\theta = a\) to \(\theta = b\).
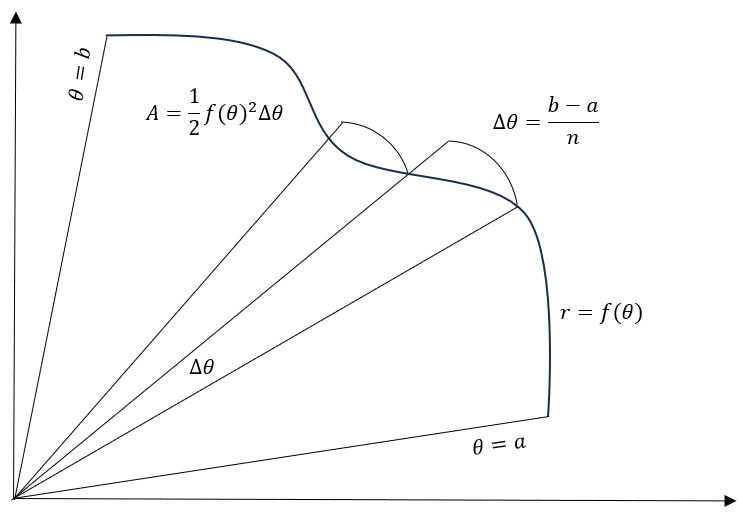
We learned in Chapter 1 (1.3.3) that the area of a circular sector of radius \(r\) over angle \(\theta\) is given by
\[A = \frac{1}{2} r^2 \theta\]
In this case, we are going to be summing over small angl the slices \(\Delta\theta\). Furthermore, the distance \(r\) from the origin is determined by our equation \(r = f(\theta)\). Therefore, the area of a single wedge is given by
\[A = \frac{1}{2}f(\theta)^2\Delta\theta\]
We will have \(n\) such circular arcs. Therefore, each \(\Delta\theta = \frac{b - a}{n}\), and the function \(f\) will be evaluated at \(\theta_i = a + i\cdot\frac{b - a}{n}\). Therefore, our Riemann Sum is given by
\[A_n = \sum_{i = 1}^{n} \frac{1}{2} f(\theta_i)^2\Delta\theta\]
Taking the limit \(n\rightarrow\infty\) on both sides, the Riemann Sum becomes an integral. Furthermore, as the circular sectors become smaller and smaller, \(\Delta\theta\) becomes the infinitesmal \(d\theta\). Therefore, our equation becomes:
\[S = \lim_{n\rightarrow\infty} A_n = \lim_{n\rightarrow\infty} \sum_{i = 1}^{n} \frac{1}{2} f(\theta_i)^2\Delta\theta = \int_{a}^{b} \frac{1}{2} f(\theta)^2 \, d\theta\]
The area under the curve of a polar equation is therefore given by
\[\begin{equation} S = \int_{\theta = a}^{\theta = b} \frac{1}{2} f(\theta)^2 \, d\theta \tag{9.6} \end{equation}\]
Examples using this formula follow.
Example 9.2 (Integrating Polar Equations) Integrate the function \(r(\theta) = 4\cos\theta\) from \(\theta = 0\) to \(\theta = \frac{\pi}{2}\).
You should recognize the equation above as a circle whose center lies along the \(x\)-axis. We simply plug what we have into equation (9.6) and evaluate the integral:
\[S = \int_{\theta = 0}^{\theta = \pi/2}\frac{1}{2}\left(4\cos\theta\right)^2 \, d\theta = 8\int_{0}^{\pi/2} \cos^2\theta \, d\theta\]
In Chapter 1 (REFERENCE HERE), we proved the trigonometric identity
\[\cos^2\theta = \frac{1 + \cos 2\theta}{2}\]
Plugging this into the integral above, we have
\[S = 4 \int_{0}^{\pi/2} (1 + \cos 2\theta) \, d\theta = 4\int_{0}^{\pi/2}\,d\theta + \int_{0}^{\pi/2} \cos 2\theta \, d\theta\]
We do the integrals separately as always. The first integral is given by
\[4\int_{0}^{\pi/2}\, d\theta = 4\theta\bigg|_{0}^{\pi/2} = 2\pi\]
We can use a \(u\)-substitution to evaluate the second integral. Letting \(u = 2\theta\) so that \(du = 2 d\theta \Rightarrow d\theta = du/2\), we have
\[\int_{0}^{\pi/2} \cos 2\theta \, d\theta = \int_{0}^{\pi} \cos u \frac{du}{2} = \frac{1}{2}\int_{0}^{\pi}\cos u \, du\]
\[= \frac{1}{2}\left[\sin u \right]_{0}^{\pi} = \frac{1}{2}\left[\sin\pi - \sin 0 \right] = 0\]
Therefore, the area of the circle is equal to \(S = 2\pi + 0 = 2\pi\). This is confirmed in the illustration below. Note that the Riemann Sum converges to the value that we just computed.
9.6 Computing Arc Lengths of Polar Functions
Finally, we can compute the arc lengths of polar curves. We need an equation we saw in Chapter 7, (7.1):
\[ds = \sqrt{dx^2 + dy^2} \]
We can perform a similar trick we used in the section on the derivatives of polar equations. Note that \(dx = \frac{dx}{d\theta} d\theta\) and \(dy = \frac{dy}{d\theta} d\theta\). Plugging these in, we have:
\[ds = \sqrt{\left(\frac{dx}{d\theta}d\theta\right)^2 + \left(\frac{dy}{d\theta} d\theta\right)^2}\]
We can pull the \(d\theta\) from both terms to obtain
\[ds = \sqrt{\left(\frac{dx}{d\theta}\right)^2 + \left(\frac{dy}{d\theta}\right)^2} d\theta\]
We already showed that \(\frac{dx}{d\theta} = \frac{dr}{d\theta}\cos\theta - r(\theta)\sin\theta\) and \(\frac{dy}{d\theta} = \frac{dr}{d\theta}\sin\theta + r(\theta)\cos\theta\). Plugging these formulas in, we have
\[ds = \sqrt{\left(\frac{dr}{d\theta}\cos\theta - r(\theta)\sin\theta\right)^2 + \left(\frac{dr}{d\theta}\sin\theta + r(\theta)\cos\theta\right)^2} d\theta\]
The reader can show that the mess under the square root can be reduced to
\[ds = \sqrt{\left(\frac{dr}{d\theta}\right)^2 + r(\theta)^2} d\theta\]
Integrating the left side will equal the arc length of the polar curve. Meanwhile, the right hand side will give us a means of actually computing the arc length. In other words, we have:
\[\begin{equation} S = \int_{\theta = a}^{\theta = b} \sqrt{\left(\frac{dr}{d\theta}\right)^2 + r(\theta)^2} \, d\theta \tag{9.7} \end{equation}\]
In this case, we are not using circular arcs but segments to approximate the length. As the segments become more and more numerous and become shorter and shorter, they more closely approximate the true length of the curve. The following figures illustrate this:
Example 9.3 (Arc Length Example) Compute the arc length of the curve \(r(\theta) = 2e^{-\theta}\) from \(\theta = 0\) to \(\theta = \infty\).
We use formula (9.7). In this case, \(a = 0\) and \(b = \infty\). Moreover, \(r(\theta) = 2e^{-\theta}\) and
\[\frac{dr}{d\theta} = -2e^{-\theta}\]
Plugging all of these pieces into our formula, we have:
\[S = \int_{0}^{\infty} \sqrt{\left(\frac{dr}{d\theta}\right)^2 + r(\theta)^2} \, d\theta = \int_{0}^{\infty} \sqrt{4e^{-2\theta} + 4e^{-2\theta}} \, d\theta\]
\[= \int_{0}^{\infty} 2\sqrt{2e^{-2\theta}} \, d\theta = 2\sqrt{2}\int_{0}^{\infty} e^{-\theta} \, d\theta\]
We found the integral of the exponential function in Chapter 5 (5.7.1). Therefore, the arc length is given by
\[S = 2\sqrt{2}\int_{0}^{\infty} e^{-\theta} \, d\theta = 2\sqrt{2}\left[-e^{-\theta}\right]_{0}^{\infty} = 2\sqrt{2} \approx 2.82843\]
The illustration below demonstrates that as the number of segments goes to infinity, the sum of the lengths of those segments converges to the value just computed. The reader is encouraged to zoom in on the center of the plot: both the red curve and the black segments which approximate them forever spiral about the origin, but the sum of the lengths of the segments converges to a finite value.